--- title: Hypothesis Testing Example - Zoetis Veterinary Research - Chi Square Test description: Hypothesis Testing Example - Use nQuery and learn how to calculate sample size and use a power analysis calculator for clinical trials. This example focuses on Zoetis Veterinary Research. image: https://www.statsols.com/hubfs/Master_Images/___HeroBannerImages/nQuery%20Sample%20Size%20Software%20Image.png --- Explore the Scientific R&D Platform ![Top Bar background texture](https://flow-cytometry.net/wp-content/uploads/2024/07/nav-bg.png) ![](https://flow-cytometry.net/wp-content/uploads/2024/07/Luma-TM.png) Scientific intelligence platform for AI-powered data management and workflow automation [Explore Luma   ](https://www.dotmatics.com/luma-data-management-platform) [![Prism logo](https://flow-cytometry.net/wp-content/uploads/2024/07/Prism-Logo-White-2.png) Statistical analysis and graphing software for scientists ](https://www.graphpad.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![Geneious logo](https://flow-cytometry.net/wp-content/uploads/2024/07/Geneious-Logo-White-2.png) Bioinformatics, cloning, and antibody discovery software ](https://www.geneious.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![SnapGene logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-SnapGene.svg) Plan, visualize, & document core molecular biology procedures ](https://www.snapgene.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![Protein Metrics logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-Protein-Metrics.svg) Proteomics software for analysis of mass spec data ](https://proteinmetrics.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![LabArchives logo](https://flow-cytometry.net/wp-content/uploads/2024/07/LabArchives-Logo-White-2.png) Electronic Lab Notebook to organize, search and share data ](https://www.labarchives.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![OMIQ logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-OMIQ.svg) Modern cytometry analysis platform ](https://www.omiq.ai/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![FCS Express logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-FCS-Express.svg) Analysis, statistics, graphing and reporting of flow cytometry data ](https://denovosoftware.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![Easy Panel logo](https://flow-cytometry.net/wp-content/uploads/2024/07/EasyPanel-Logo-White-2.png) Intelligent panel design & inventory management for flow cytometry ](https://flow-cytometry.net/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![nQuery logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-nQuery.svg) Software to optimize designs of clinical trials ](https://www.statsols.com/) [![M-Star logo](https://flow-cytometry.net/wp-content/uploads/2024/07/M-Star-Logo-White-2.png) Computational fluid dynamics (CFD) software for engineers and researchers ](https://www.mstarcfd.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![SoftGenetics logo](https://flow-cytometry.net/wp-content/uploads/2024/07/SoftGenetics-Logo-White-2.png) Genetic analysis software for research, forensics & healthcare applications ](https://softgenetics.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [Explore the Scientific Software   ](https://www.dotmatics.com/portfolio) [![nQuery Logo](https://www.statsols.com/hubfs/nQuery%20Logo.svg "nQuery Logo")](https://www.statsols.com/) [![Pricing](https://no-cache.hubspot.com/cta/default/488764/23ddd076-07af-4f0a-9388-5a58a5369002.png)](https://cta-redirect.hubspot.com/cta/redirect/488764/23ddd076-07af-4f0a-9388-5a58a5369002) [![Free Trial](https://no-cache.hubspot.com/cta/default/488764/93ddde0f-93b2-4893-a3db-0523d2334739.png)](https://cta-redirect.hubspot.com/cta/redirect/488764/93ddde0f-93b2-4893-a3db-0523d2334739) # Sample Size Determination Example ## AREA: Proportions | Veterinary ![nQuery In Use Background Web Opacity 35](https://www.statsols.com/hs-fs/hubfs/Master_Images/___HeroBannerImages/nQuery%20In%20Use%20Background%20Web%20%20Opacity%2035.png?width=1920&name=nQuery%20In%20Use%20Background%20Web%20%20Opacity%2035.png "nQuery In Use Background Web Opacity 35") #### Zoetis Veterinary Research #### Title: Bovine viral diarrhoea virus in beef heifers in commercial herds in Australia: mob-level seroprevalences and incidences of seroconversion, and vaccine efficacy **Objective: **To describe management group (mob)‐level seroprevalences and incidences of seroconversion to bovine viral diarrhoea virus (BVDV), and to determine the efficacy of a vaccine against BVDV, in beef heifers in commercial herds in Australia. **Year:** 2013 **Source:** New England Journal of Medicine **Link: **[http://onlinelibrary.wiley.com/doi/10.1111/avj.12129/abstract](http://onlinelibrary.wiley.com/doi/10.1111/avj.12129/abstract) **Clinical Area: **Veterinary (Bovine) | **Sample Size Section in Paper/Protocol:** | | --- | | “We planned to enrol 2500 heifers (1250 each of Pestigard®- and placebo-treated heifers). Statistical power calculations indicated that the trial would have had power of 0.72, 0.73 and 0.91 for detecting a significant difference at the 0.05 level (two-sided) in proportions of heifers that were pregnant by 6 weeks between Pestigard® and placebo treated heifers, if the proportions in the placebo-treated heifers were 40%, 60% and 80%, respectively, and if Pestigard® treatment increases these proportions by 0.05 (i.e. 5 percentage points). If the increase is 0.10 (i.e. 10 percentage points), statistical power would have been 1.00. Power for detecting differences in proportions of heifers with calves at branding or weaning of 5 and 10 percentage points would have been 0.91 and 1.00 if 80% and 90% of the placebo-treated heifers had a calf at branding and weaning, respectively. 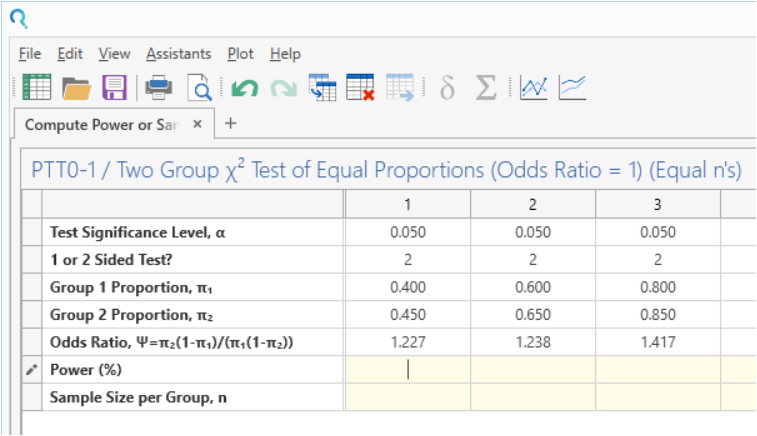Sample size calculations were performed using WinPepi[10] and did not account for clustering of heifer within mob as the numbers of Pestigard®- and placebo-treated heifers were to be very similar so there would be minimal impact of clustering on variance inflation factors.” | ** Summary of Necessary Parameter Estimates for Sample Size Calculation:** |  Parameter | 40% | 60% | 80% | | --- | --- | --- | --- | |  Significance Level (2-Sided) | 0.05 | 0.05 | 0.05 | |  Control Proportion | 0.4 | 0.6 | 0.8 | |  Treatment Proportion | 0.45 | 0.65 | 0.85 | |  Sample Size Per Group | 1250 | 1250 | 1250 | *** Note: that clustering was not taken into account in this analysis. 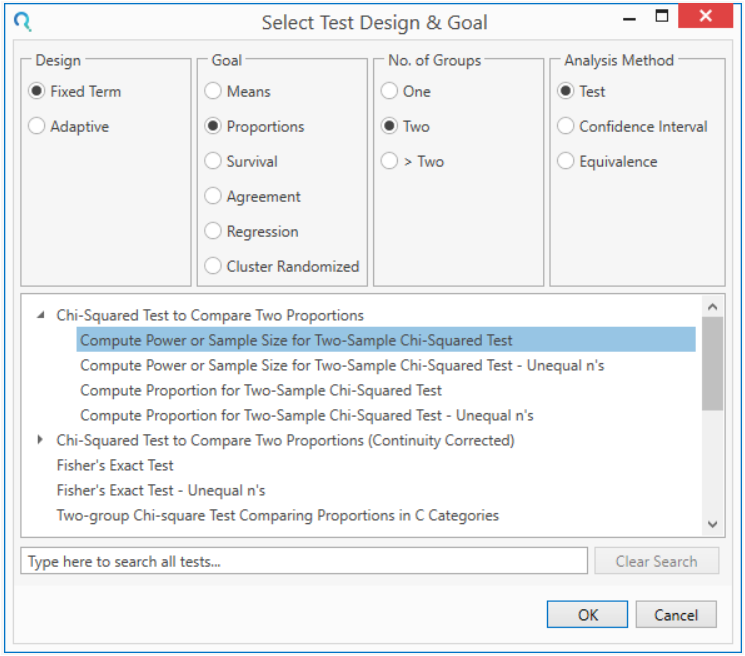Our cluster ******randomised table would allow investigators to easily investigate the effect it could ******have had on the power estimate and prevent an underpowered study.*** #### **Email me this example in PDF format** **Step 1: **Select the table ***Compute Power or Sample Size for Two-Sample Chi-Squared Test ***from the Select Test Design & Goal window. This is located under the **Chi-Squared Test to Compare Two Proportions** dropdown This can be done **using the radio buttons** or alternatively, you can** use the search bar** at the end of the Select Test Design & Goal window. ![Sample Size Calculator Example- nQuery- Example 18- Img 01- Compute Power or Sample Size for Two-Sample Chi-Squared Test](https://www.statsols.com/hs-fs/hubfs/Master_Images/___PageImages/Worked%20Examples/nQuery%20Example%20Images/Sample%20Size%20Calculator%20Example-%20nQuery-%20Example%2018-%20Img%2001-%20Compute%20Power%20or%20Sample%20Size%20for%20Two-Sample%20Chi-Squared%20Test.png?width=745&name=Sample%20Size%20Calculator%20Example-%20nQuery-%20Example%2018-%20Img%2001-%20Compute%20Power%20or%20Sample%20Size%20for%20Two-Sample%20Chi-Squared%20Test.png) **Step 2: **Enter the parameter values for sample size calculation taken from the study design. ![Sample Size Calculator Example- nQuery- Example 18- img 02- Compute Power or Sample Size for Two-Sample Chi-Squared Test](https://www.statsols.com/hs-fs/hubfs/Master_Images/___PageImages/Worked%20Examples/nQuery%20Example%20Images/Sample%20Size%20Calculator%20Example-%20nQuery-%20Example%2018-%20img%2002-%20Compute%20Power%20or%20Sample%20Size%20for%20Two-Sample%20Chi-Squared%20Test.png?width=757&name=Sample%20Size%20Calculator%20Example-%20nQuery-%20Example%2018-%20img%2002-%20Compute%20Power%20or%20Sample%20Size%20for%20Two-Sample%20Chi-Squared%20Test.png) **Step 3: **Enter the sample size. Once the sample size is entered, the power is calculated automatically. Make sure ***‘Calculate the power’ ***is selected from the action dropdown menu. 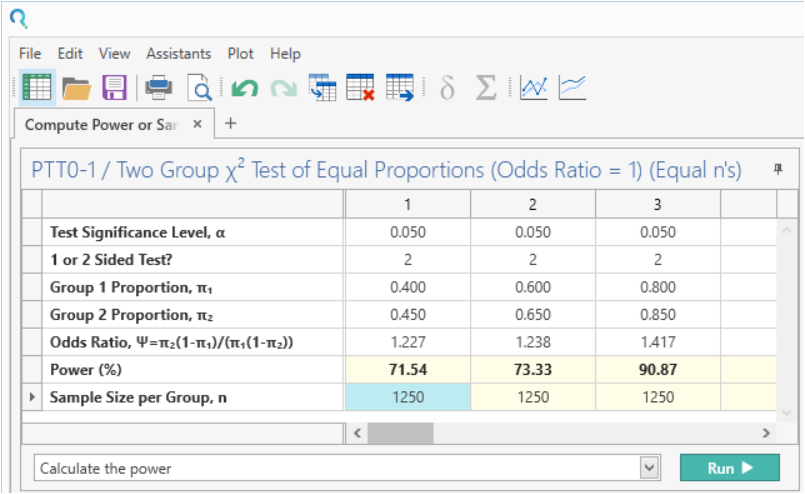![Sample Size Calculator Example- nQuery- Example 18- img 03- Compute Power or Sample Size for Two-Sample Chi-Squared Test](https://www.statsols.com/hs-fs/hubfs/Master_Images/___PageImages/Worked%20Examples/nQuery%20Example%20Images/Sample%20Size%20Calculator%20Example-%20nQuery-%20Example%2018-%20img%2003-%20Compute%20Power%20or%20Sample%20Size%20for%20Two-Sample%20Chi-Squared%20Test.png?width=805&name=Sample%20Size%20Calculator%20Example-%20nQuery-%20Example%2018-%20img%2003-%20Compute%20Power%20or%20Sample%20Size%20for%20Two-Sample%20Chi-Squared%20Test.png) | This gives rounded powers of 72%, 73% & 91% as per the study design Statement. | | --- | ** Step 4: **An output statement is available for each scenario. Just click the corresponding column to get the output statement for that scenario. The output statement appears at the bottom of nQuery. This can be printed or copy and pasted into any document. | Output Statement: | | --- | | *“**A two group χ² test with a 5% two-sided significance level will have 73.33% power to detect the difference between a Group 1 proportion, π₁, of 0.6 and a Group 2 proportion, π₂ of 0.65 (odds ratio of 1.238) when the sample size in each group is 1250..”* |   ![Example 18 Img 04](https://www.statsols.com/hs-fs/hubfs/Master_Images/___PageImages/Worked%20Examples/nQuery%20Example%20Images/Example%2018%20Img%2004.png?width=735&name=Example%2018%20Img%2004.png) #### **Email me this example in PDF format** ### Free 14 Day Trial ![Demo Icon white](https://www.statsols.com/hs-fs/hubfs/Demo%20Icon%20white.png?width=330&name=Demo%20Icon%20white.png) **No download required**   [Try Now](https://www.statsols.com/nquery-demo) ##### **LOCATION** GraphPad Software DBA Statistical Solutions, 225 Franklin St FL 26 Boston, MA, 02110-2853, United States Copyright © Statsols. All Rights Reserved. [Do Not Sell or Share My Personal Information](https://donotsell.dotmatics.com/hc/en-us/requests/new). [Privacy Policy](https://www.statsols.com/privacy-policy?hsLang=en-us) .