--- title: Sample Size Determination for Andersen-Gill Recurrent Events in Immunology | Statistics in Medicine description: Learn how to determine sample sizes for clinical trials using the Andersen-Gill model. Get insights on calculating rates of recurrent events in immunology research. image: https://www.statsols.com/hubfs/Master_Images/___HeroBannerImages/nQuery%20Sample%20Size%20Software%20Image.png --- Explore the Scientific R&D Platform ![Top Bar background texture](https://flow-cytometry.net/wp-content/uploads/2024/07/nav-bg.png) ![](https://flow-cytometry.net/wp-content/uploads/2024/07/Luma-TM.png) Scientific intelligence platform for AI-powered data management and workflow automation [Explore Luma   ](https://www.dotmatics.com/luma-data-management-platform) [![Prism logo](https://flow-cytometry.net/wp-content/uploads/2024/07/Prism-Logo-White-2.png) Statistical analysis and graphing software for scientists ](https://www.graphpad.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![Geneious logo](https://flow-cytometry.net/wp-content/uploads/2024/07/Geneious-Logo-White-2.png) Bioinformatics, cloning, and antibody discovery software ](https://www.geneious.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![SnapGene logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-SnapGene.svg) Plan, visualize, & document core molecular biology procedures ](https://www.snapgene.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![Protein Metrics logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-Protein-Metrics.svg) Proteomics software for analysis of mass spec data ](https://proteinmetrics.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![LabArchives logo](https://flow-cytometry.net/wp-content/uploads/2024/07/LabArchives-Logo-White-2.png) Electronic Lab Notebook to organize, search and share data ](https://www.labarchives.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![OMIQ logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-OMIQ.svg) Modern cytometry analysis platform ](https://www.omiq.ai/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![FCS Express logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-FCS-Express.svg) Analysis, statistics, graphing and reporting of flow cytometry data ](https://denovosoftware.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![Easy Panel logo](https://flow-cytometry.net/wp-content/uploads/2024/07/EasyPanel-Logo-White-2.png) Intelligent panel design & inventory management for flow cytometry ](https://flow-cytometry.net/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![nQuery logo](https://cdn.labarchives.com/assets/16.23.0/assets/images/dotmatics/lab-archives/top-bar/PreNav-Logo-nQuery.svg) Software to optimize designs of clinical trials ](https://www.statsols.com/) [![M-Star logo](https://flow-cytometry.net/wp-content/uploads/2024/07/M-Star-Logo-White-2.png) Computational fluid dynamics (CFD) software for engineers and researchers ](https://www.mstarcfd.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [![SoftGenetics logo](https://flow-cytometry.net/wp-content/uploads/2024/07/SoftGenetics-Logo-White-2.png) Genetic analysis software for research, forensics & healthcare applications ](https://softgenetics.com/?utm_medium=referral&utm_source=nquery&utm_campaign=dotmatics-top-bar) [Explore the Scientific Software   ](https://www.dotmatics.com/portfolio) [![nQuery Logo](https://www.statsols.com/hubfs/nQuery%20Logo.svg "nQuery Logo")](https://www.statsols.com/) [![Pricing](https://no-cache.hubspot.com/cta/default/488764/23ddd076-07af-4f0a-9388-5a58a5369002.png)](https://cta-redirect.hubspot.com/cta/redirect/488764/23ddd076-07af-4f0a-9388-5a58a5369002) [![Free Trial](https://no-cache.hubspot.com/cta/default/488764/93ddde0f-93b2-4893-a3db-0523d2334739.png)](https://cta-redirect.hubspot.com/cta/redirect/488764/93ddde0f-93b2-4893-a3db-0523d2334739) # Sample Size Determination Example ## AREA: Andersen-Gill, Recurrent Events | Immunology ![nQuery In Use Background Web Opacity 35](https://www.statsols.com/hs-fs/hubfs/Master_Images/___HeroBannerImages/nQuery%20In%20Use%20Background%20Web%20%20Opacity%2035.png?width=1920&name=nQuery%20In%20Use%20Background%20Web%20%20Opacity%2035.png "nQuery In Use Background Web Opacity 35") ##### Andersen-Gill (Recurrent Events) Worked Examples #### Title: Sample size calculation for the Andersen-Gill model comparing rates of recurrent events **Objective: **CGD is a rare immune system disorder characterized by recurrent pyogenic infections. Suppose we want to design a new trial to assess the effect of a new experimental product on the infection rate. (Example 1). **Year:** 2019 **Source:** Statistics in Medicine **Link:** https://onlinelibrary.wiley.com/doi/abs/10.1002/sim.8335 **Clinical Area:** Immunology | **Sample Size Section in Paper/Protocol:** | | --- | | Suppose we want to design a new trial to assess the effect of a new experimental product on the infection rate. We assume that the event rate function is of Weibull form λ 0 (t) = ψνt ν−1 in the placebo arm, and the event rate ratio between the two treatments is constant λ 1 (t)∕λ 0 (t) = exp(β) = 0.6 over time. We get the MLE (ψ, ν, κ)=(1.097 1.221 , 1.221, 0.871) by fitting an NB process model to the data using the SAS NLMIXED procedure on basis of the likelihood function given in Equation (20) of Dean and Balshaw. Matsui obtained similar point estimates based on the generalized estimating equations (GEE) for the MPP To determine the sample size, we assume a common dispersion parameter and identical dropout pattern in the two groups. We set ψ = 1.1, ν = 1.2, κ = 0.8, which are close to the MLE. The treatment allocation ratio is p1 ∶ p0 = 1 ∶ 1 or 2 ∶ 1. Both design 1 (planned treatment duration τc = 1 year for all patients) and design 2 (accrual period τa = 0.5 year, additional treatment duration τc = 1 year, constant enrollment rate η = 0) are considered. In both designs, the loss to follow-up distribution is exponential with mean 1∕δ = 4 years. The sample sizes for these designs are as follows: **Design 1 Balanced:** 365, Design 1 Unbalanced (2:1): 390 **Design 2 Balanced:** 335, Design 2 Unbalanced (2:1): 360 | ** Summary of Necessary Parameter Estimates for Sample Size Calculation:** | ** Parameter** | **Value** | | --- | --- | | Significance Level (2-Sided) | 0.1 | | Weibull Scale | 1.1 | | Weibull Shape | 1.2 | | Event Rate Ratio | 0.6 | | Dispersion Parameter (both groups) | 0.8 | | Exponential Dropout Rate | 0.25 | | Power | 90 | | Minimum Treatment Period | 1 | | Accrual Period (Design 1;Design 2) | 0;0.5 (enrollment = 0) | | Sample Size Allocation (balanced/unbalanced) | 0.5;0.333 (1:1;1:2)  |   #### **Email me this example in PDF format** **Step 1: **Select the **MTT44 Inequality Tests for the Ratio of Two Incidence Rates using Andersen-Gill Model** table from the Select Test window. This can be done **using the radio buttons below** or alternatively, you can **use the search bar** at the end of the Select Test window and search for terms such as “MTT44” or “Andersen” and select the correct table. After selecting the table in the window below the radio buttons, select OK to open the table. ![Andersen-Gill - Recurrent Events - Sample Size Example_Page_4_Image_0001](https://www.statsols.com/hs-fs/hubfs/Master-Images/Page-Images/Worked-Examples/nQuery%20Example%20Images/Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_4_Image_0001.jpg?width=775&name=Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_4_Image_0001.jpg) **Step 2: **To replicate this example, the first four columns will be used for the balanced and unbalanced (1:2 controls:treatment) versions of Design 1 (no accrual period) and 2 (6 month accrual period). 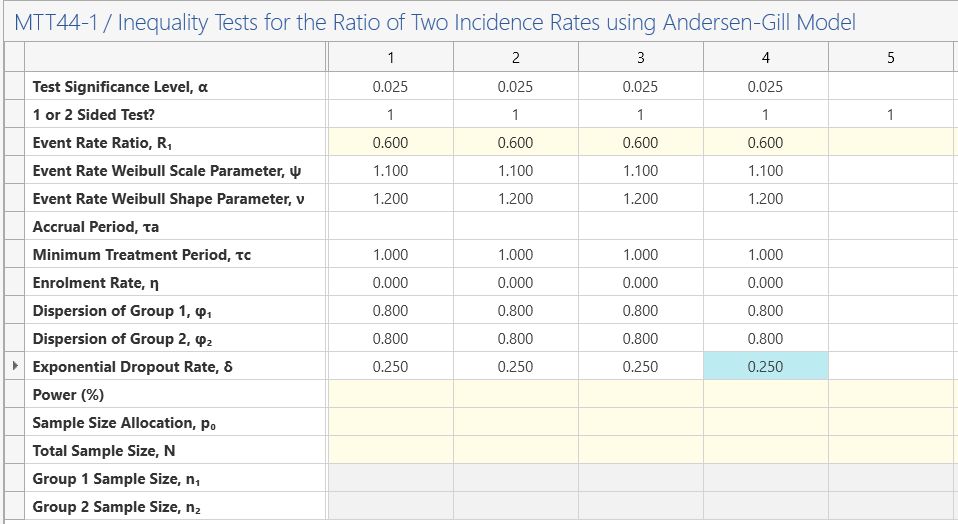The following parameters are the same in each column: Enter the significance level of 0.025 and select a 1-sided analysis. Enter the event rate ratio of 0.6, the Weibull Scale parameter of 1.1 and the Weibull Shape parameter of 1.2. As the minimum treatment period is the same for each design, enter 1 in the minimum treatment row in each column. As the enrollment rate will be ignored for the case where accrual equals zero, set this value to 0 (uniform accrual) in each column. Enter the group 1 and 2 dispersion as 0.8 as these are assumed to be the same in each group in the study design. Enter 0.25 for the exponential dropout rate. Note this is equivalent to the δ in the design above, where 1/δ = 4 years (equivalent to 21% dropout per year). 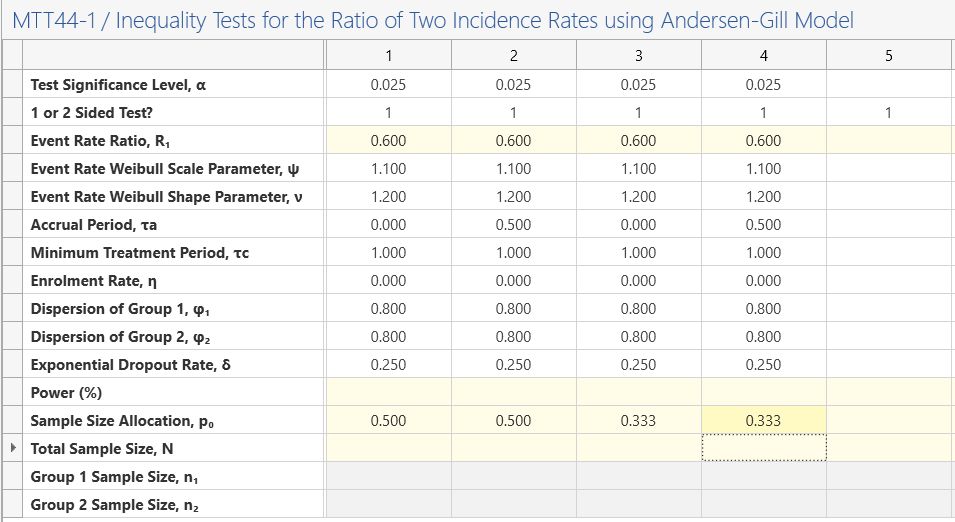![Andersen-Gill - Recurrent Events - Sample Size Example_Page_5_Image_0001](https://www.statsols.com/hs-fs/hubfs/Master-Images/Page-Images/Worked-Examples/nQuery%20Example%20Images/Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_5_Image_0001.jpg?width=958&name=Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_5_Image_0001.jpg) The balanced design 1, balanced design 2, unbalanced design 1 and unbalanced design 2 will be entered into columns 1-4 respectively. In columns 1 and 3, enter an accrual period of zero. In columns 2 and 4, enter an accrual period of 0.5. In columns 1 and 2, enter a sample size allocation of 0.5. In columns 3 and 4, enter a sample size allocation of 0.33333333. **![Andersen-Gill - Recurrent Events - Sample Size Example_Page_6_Image_0001](https://www.statsols.com/hs-fs/hubfs/Master-Images/Page-Images/Worked-Examples/nQuery%20Example%20Images/Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_6_Image_0001.jpg?width=955&name=Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_6_Image_0001.jpg)** **Step 3: **Enter the power of 90% in each column and the Total Sample Size and per group sample sizes will be calculated. **![Andersen-Gill - Recurrent Events - Sample Size Example_Page_7_Image_0001](https://www.statsols.com/hs-fs/hubfs/Master-Images/Page-Images/Worked-Examples/nQuery%20Example%20Images/Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_7_Image_0001.jpg?width=954&name=Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_7_Image_0001.jpg)** | **Result:** | | --- | | The analysis results in a sample sizes of 365, 335, 390 and 360 as per Table 1 in the paper. | We can summarize our results by using the output statement. ![Andersen-Gill - Recurrent Events - Sample Size Example_Page_7_Image_0002](https://www.statsols.com/hs-fs/hubfs/Master-Images/Page-Images/Worked-Examples/nQuery%20Example%20Images/Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_7_Image_0002.jpg?width=1188&name=Andersen-Gill%20-%20Recurrent%20Events%20-%20Sample%20Size%20Example_Page_7_Image_0002.jpg) #### **Email me this example in PDF format** ### Free 14 Day Trial ![Demo Icon white](https://www.statsols.com/hs-fs/hubfs/Demo%20Icon%20white.png?width=330&name=Demo%20Icon%20white.png) **No download required**   [Try Now](https://www.statsols.com/nquery-demo) ##### **LOCATION** GraphPad Software DBA Statistical Solutions, 225 Franklin St FL 26 Boston, MA, 02110-2853, United States Copyright © Statsols. All Rights Reserved. [Do Not Sell or Share My Personal Information](https://donotsell.dotmatics.com/hc/en-us/requests/new). [Privacy Policy](https://www.statsols.com/privacy-policy?hsLang=en-us) .