Pricing
Free Trial

Sample Size Determination Example

AREA: Unblinded SSR, Two Proportions | Cardiology

nQuery In Use Background Web Opacity 35
Unblinded Sample Size Re-estimation - Two Proportions Worked Examples

Title: Levosimendan for Hemodynamic Support after Cardiac Surgery

Objective: Acute left ventricular dysfunction is a major complication of cardiac surgery and is
associated with increased mortality. Meta-analyses of small trials suggest that levosimendan may result in a higher rate of survival among patients undergoing cardiac surgery.

Year: 2017

Source: The New England Journal of Medicine

Link: https://www.nejm.org/doi/suppl/10.1056/NEJMoa1616325/suppl_file/nejmoa1616325_protocol.
pdf

Clinical Area: Cardiology

Sample Size Section in Paper/Protocol:

“The sample-size calculation was based on a two-sided alpha error of 0.05 and 80% power. On the basis of meta-analyses that estimated that mortality would be reduced from 12.7% to 4.7% with levosimendan use, we expected 10% mortality in the placebo group and 5% mortality in the levosimendan group. Accordingly, we calculated that a sample of 435 patients per group was needed. In order to account for protocol deviations and withdrawal of consent, we planned for 500 patients per group to undergo randomization. Interim analyses were planned after enrollments of 25% and 50% of the sample size.”


Summary of Necessary Parameter Estimates for Sample Size Calculation:

 Parameter Value
Significance Level (2-Sided) 0.05
Placebo Proportion 0.05
Treatment Proportion 0.1
Power 80%
Number of looks 3
(at 25%, 50% and 100% of the sample size)
Alpha Spending Function O’Brien-Fleming

 

Email me this example in PDF format

Step 1:
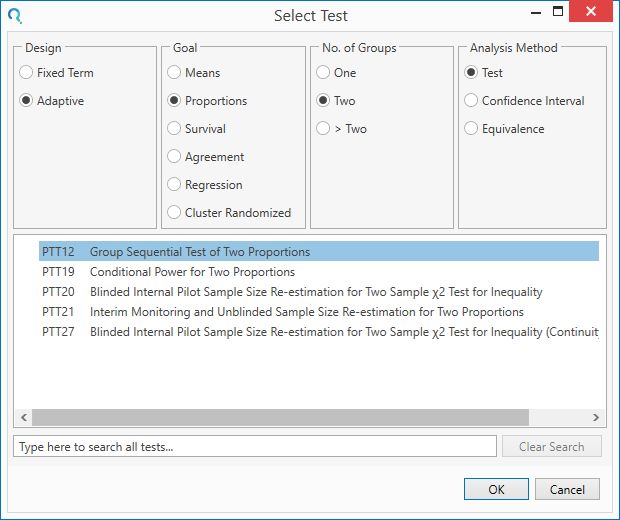
Select the PTT12 Group Sequential Test of Two Proportions table from the Select Test window.

This can be done using the radio buttons below or alternatively, you can use the search bar at the end of the Select Test window.

Unblinded Sample Size Re-estimation - Two Proportions - Sample Size 1

Step 2:
Enter the significance level and group proportion parameter values taken from the study design.

(Note that the odds ratio will automatically calculate based on the group proportions while the
default values for Continuity Correction and Variance are used.)

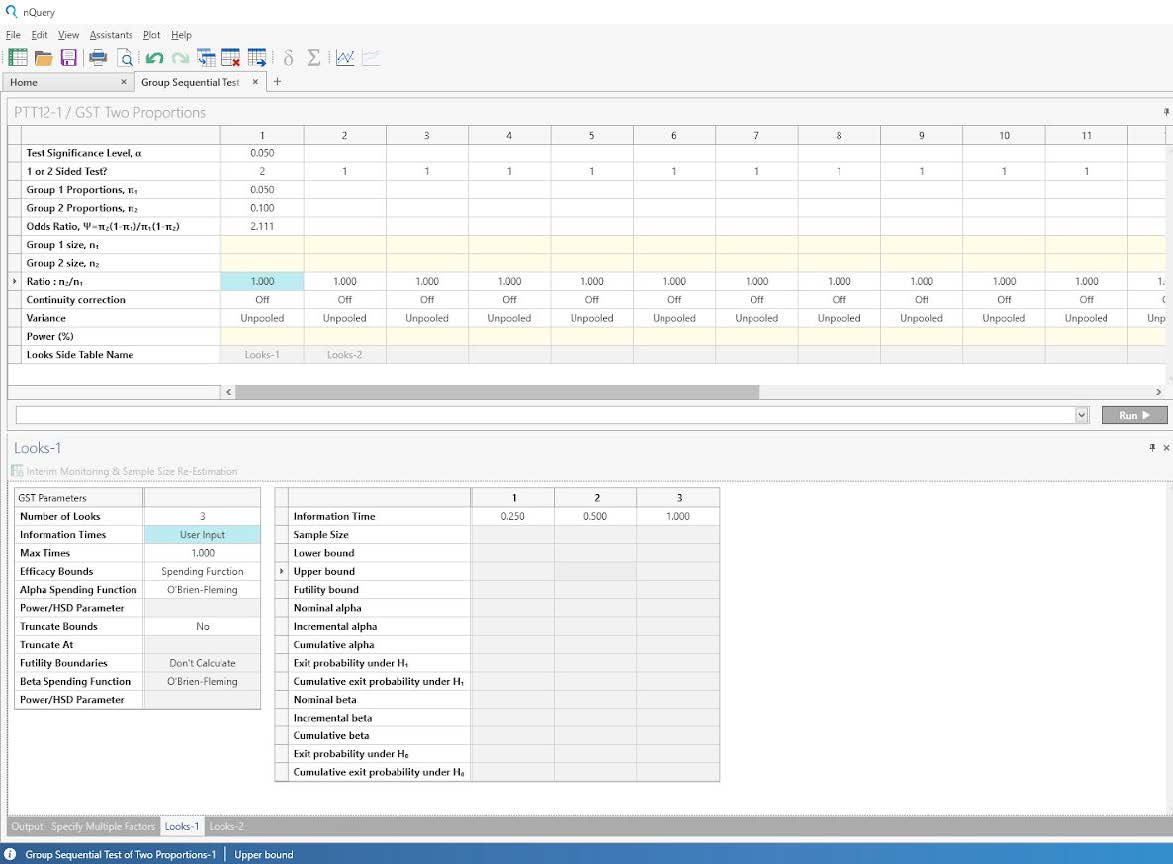
Unblinded Sample Size Re-estimation - Two Proportions - Sample Size 2

Step 3:
Complete the looks side-table using the values taken from the study design.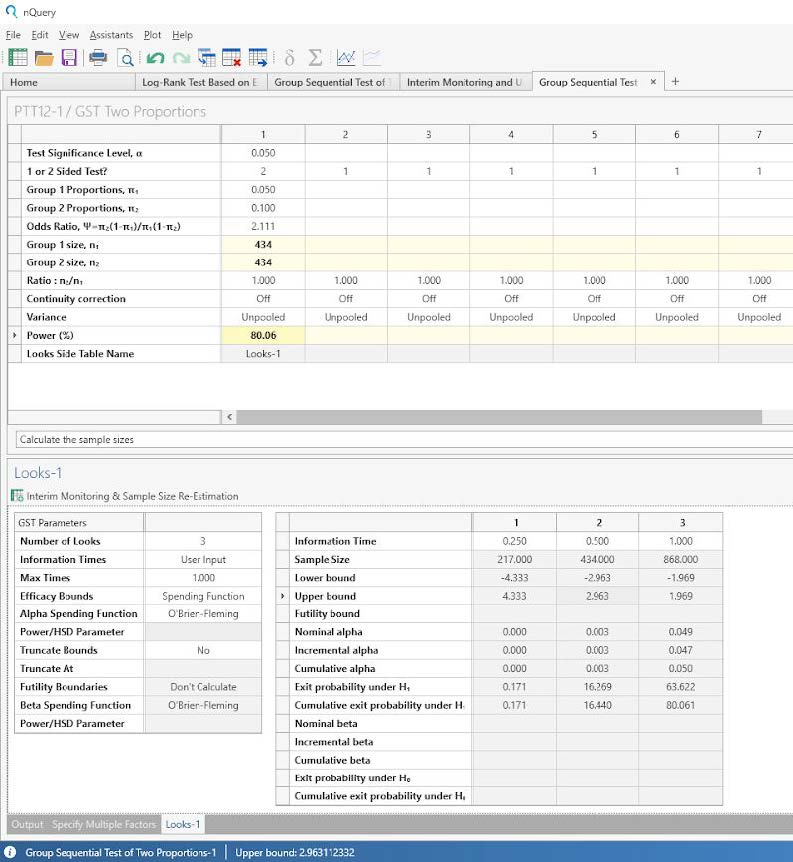Unblinded Sample Size Re-estimation - Two Proportions - Sample Size 4

Step 4:
Enter the power for the test and the sample size and looks-side table will be completed.

Unblinded Sample Size Re-estimation - Two Proportions - Sample Size 4

The analysis results in a sample size per group of 434. This is very similar to the sample size per group of 435 stated in the protocol and the difference is likely due to rounding.

The power of the test is 80.06%.

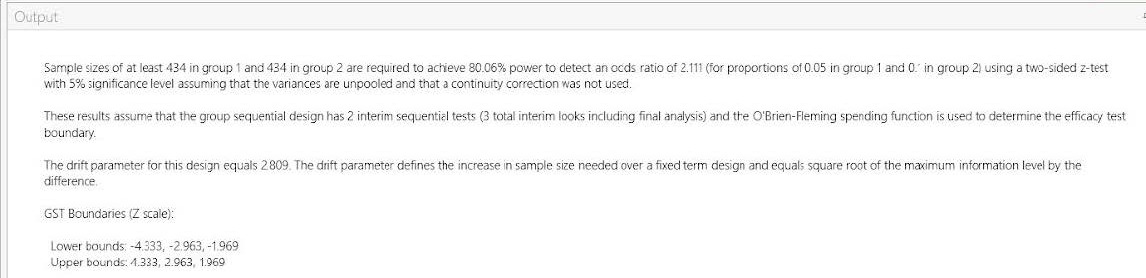
Output Statement:

“Sample sizes of at least 434 in group 1 and 434 in group 2 are required to achieve 80.06%
power to detect an odds ratio of 2.111 (for proportions of 0.05 in group 1 and 0.1 in group 2)
using a two-sided z-test with 5% significance level assuming that the variances are unpooled and that a continuity correction was not used.

These results assume that the group sequential design has 2 interim sequential tests (3 total
interim looks including final analysis) and the O'Brien-Fleming spending function is used to
determine the efficacy test boundary.

The drift parameter for this design equals 2.809. The drift parameter defines the increase in
sample size needed over a fixed term design and equals square root of the maximum
information level by the difference.


GST Boundaries (Z scale):
Lower bounds: -4.333, -2.963, -1.969
Upper bounds: 4.333, 2.963, 1.969”

Unblinded Sample Size Re-estimation - Two Proportions - Sample Size 5


This study can be extended to demonstrate an Unblinded Sample Size Re-estimation with Interim Monitoring.

Suppose we wanted to monitor the trial at each look and consider a sample size re-estimation at the second look.

Using the same group sequential design, suppose that the interim placebo
proportion was 0.06 (an increase of 20% from 0.05 ) and that the interim treatment proportion
remained at 0.1.

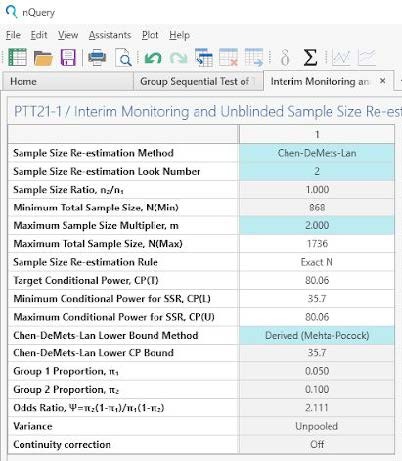
We will use the Chen-DeMets-Lan re-estimation method, the maximum events multiplier will be 2 and we will use the derived Chen-DeMets-Lan lower bound method.

Additional Parameter Estimates for Unblinded SSR:
 Parameter Value
Events Re-estimation Method Chen-DeMets-Lan
Events Re-estimation Look Number 2
Maximum Events Multiplier 2
Chen-DeMets-Lan Lower Bound Method Derived (Mehta-Pocock)
Interim Placebo Proportion 0.06 (at all 3 looks)
Interim Treatment Proportion 0.1


Step 1:
Click the “Interim Monitoring & Sample Size Re-estimation” button on the PTT12 looks side table to open the PTT21 Interim Monitoring and Unblinded Sample Size Re-estimation for two Proportions table.

interim looks

Step 2: 
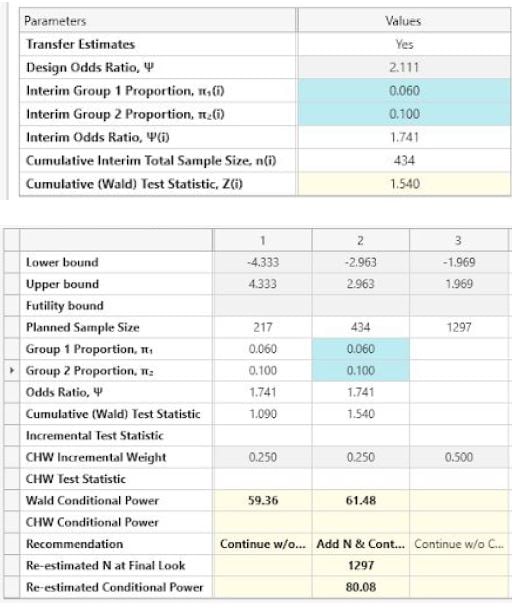
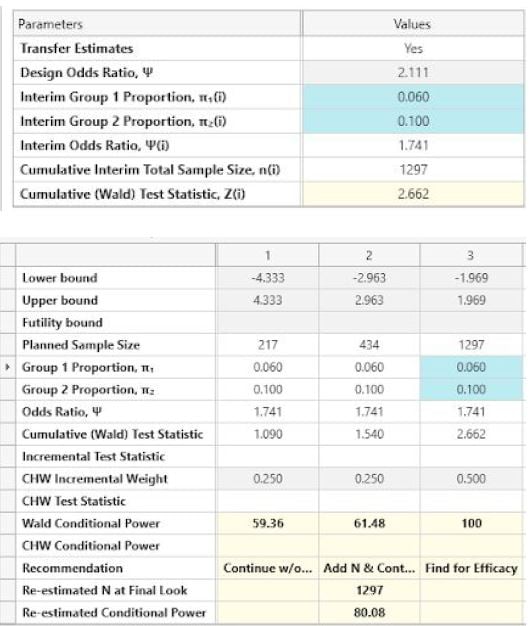
Use the Unblinded SSR parameter estimates to complete the first table.

Unblinded Sample Size Re-estimation - Two Proportions - Sample Size 7

Step 3:
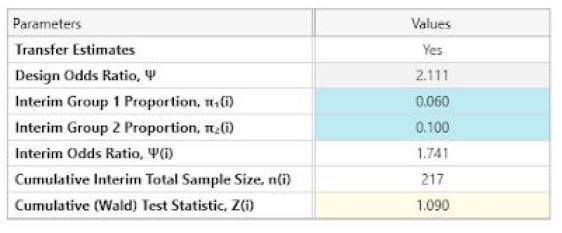
Use the side table to enter the Interim group proportions at all 3 looks.
Note: Ensure that “Transfer Estimates” is set to Yes.

The following is output at each look.

Look 1

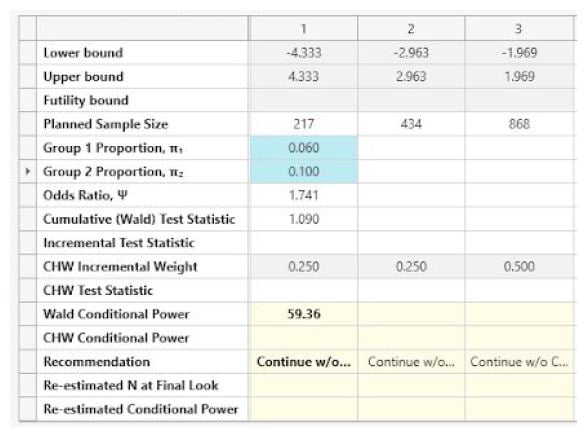
Unblinded Sample Size Re-estimation - Two Proportions - look1Unblinded Sample Size Re-estimation - Two Proportions - look1b

The test statistic of 1.09 is not significant.

Look 2

 

Unblinded Sample Size Re-estimation - Two Proportions - look2

The test statistic of 1.54 is not significant. The conditional power is between 35.7 & 80.1 so a sample size increase is applied.

Here the sample size is increased to 1297.

Look 3

 

Unblinded Sample Size Re-estimation - Two Proportions - look3

Result


The test statistic of 2.66 is significant,
so we find for efficacy at the final analysis.

 

Email me this example in PDF format

Free 14 Day Trial
Demo Icon white
No download required
 
LOCATION
GraphPad Software DBA Statistical Solutions, 225 Franklin St FL 26 Boston, MA, 02110-2853, United States

Copyright © Statsols. All Rights Reserved. Do Not Sell or Share My Personal Information. Privacy Policy .