Binary Outcome Trials (Proportion data)
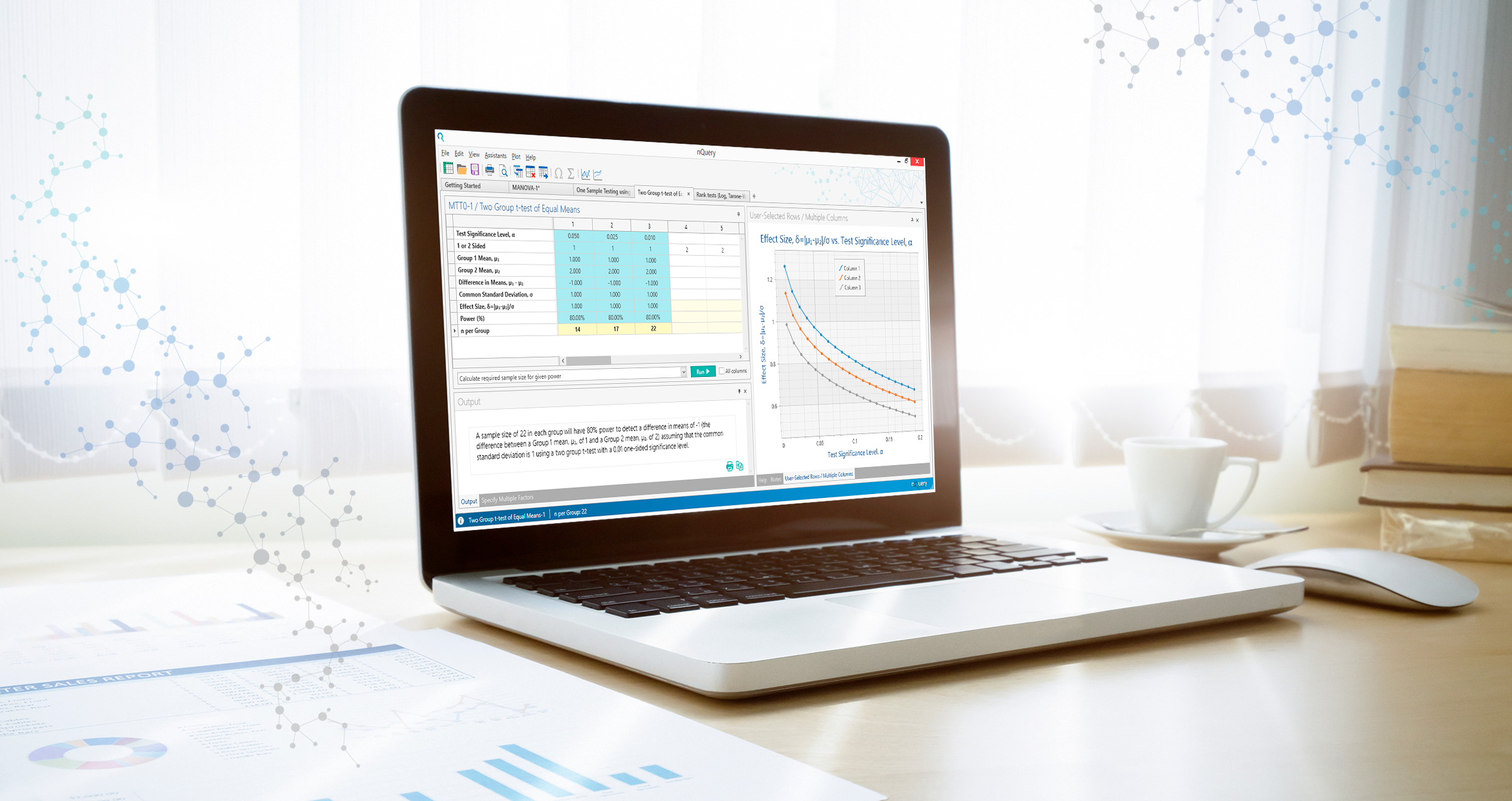
Binary data is one of the most common data forms used as an endpoint for clinical trials. Binary data can result from almost any sort of trial where “success” and “failure” can be explicitly defined.
Common design types in this context would be one-sample, paired and parallel studies. In the context of binary data, one of the most noticeable aspects is the wide variety of options available ranging from relatively simple normal approximation tests to more complex exact methods and sample size methods have followed this trend in regard to binary data analyses generally.
This release will bring 9 new tables that deal with different trial designs with binary endpoints, extending the range of designs for proportions data already on offer.
These tables fall into three broad categories:
- Wald Tests for Logistic Regression
- Equivalence Tests for Correlated Proportions
Wald Tests for Logistic Regression
These tables give further methods to characterise the effect of a binary variable on an outcome. Logistic regression is used to explain the relationship between a binary response variable and one or more explanatory or exposure variables. Logistic regression is used in particular, rather than linear regression, when the response variable is categorical in nature. For example, an exposure variable may be whether a subject smoked or not, while the response variable may be the presence or absence of cancer in the subject.
The Wald test is then used to test the significance of an exposure variable, or an interaction between an exposure variable and some other confounding variable. Calculations are made according to the method outlined by Demidenko (2007).
In the latest nQuery release we are adding 6 new tables in this area:
- Wald Test for the Odds Ratio in Logistic Regression with One Binary Covariate
- Wald Test for the Odds Ratio in Logistic Regression with Two Binary Covariates
- Wald Test for the Interaction Odds Ratio in Logistic Regression with Two Binary Covariates
- Confidence Interval for the Odds Ratio in Logistic Regression with One Binary Covariate
- Wald Test for the Odds Ratio in Logistic Regression with Two Binary Covariates
- Confidence Interval for the Interaction Odds Ratio in Logistic Regression with Two Binary Covariates
These tables add to the range of logistic regression methods already available in nQuery, and allow versatility with significance tests in addition to confidence interval tables available.
Equivalence Tests
In this release, there is also a focus on equivalence tests for binary data. Equivalence testing is used to statistically evaluate how similar a proposed treatment is to a pre-existing standard treatment. This is a very common objective in areas such as generics and medical devices. This is particularly important if using a placebo group.
As equivalence testing will typically involve evaluation against a well-defined treatment (e.g. RLD), there is a lower incidence of the large parallel studies typically seen in Phase III clinical trials. One-sample, paired samples or cross-over designs are common as these will generally require a lower cost and sample size.
Three tables will be added in this area in the latest release:
- Equivalence Test for One Proportion
- Difference Equivalence Test for Two Correlated Proportions
- Ratio Equivalence Test for Two Correlated Proportions
These tables integrate more exact enumeration methods as an option in addition to the typical normal approximation methods. The one proportion test also includes a wide range of proposed test statistics, including an exact test and a variety of forms of Z-test.
Correlated proportions often occur where two different procedures, such as diagnostic tests, are carried out on all subjects in order to test the accuracy of the procedure. A level of correlation between the results would be expected in this situation. In equivalence tests with correlated proportions, the aim is to show that the two diagnostic procedures have the same level of accuracy.
These tables expand upon a large number of pre-existing tables available for the equivalence testing of binary proportions.
Continue to explore the new Core tables by clicking on the tabs above