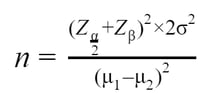Step 5. Explore Parameter Uncertainty
Once steps 1 to 4 have been completed, and the appropriate sample size or relevant power has been found, you can move onto step 5 which is to explore the uncertainty in your sample size design.
The unknown parameters and effect size that have been defined in steps 2 and 3 are just that - estimates. It is not known what the true value of these parameters should be. If all these parameters were known, there would be no need to run the clinical trial! If the parameters are inaccurate, we risk the possibility of underpowering the study and not having a large enough sample size to find the effect size or we may overpower and subject too many people to what may be an ineffective treatment.
Traditionally, this uncertainty would have been explored primarily using sensitivity analysis. A sensitivity analysis is a part of planning a clinical trial that is easily forgotten but is extremely important for regulatory purposes and publication in peer-reviewed journals. It involves analyzing what effect changing the assumptions from parts 2, 3 and 4 would have on the sample size or power in the particular sample size or power calculation. This is important as it helps in understanding the robustness of the sample size estimate and dispels the common overconfidence in that initial estimate.
Some parameters have a large degree of uncertainty about them. For example, the intra-cluster correlation is often very uncertain when based on the literature or a pilot study, and so it’s useful to look at a large range of values for that parameter to see what effect that has on the resulting sample size. Moreover, some analysis parameters will have a disproportionate effect on the final sample size, and therefore seeing what effect even minor changes in those parameters would have on the final sample size is very important.
When conducting a sensitivity analysis, a choice has to be made over how many scenarios will be explored and what range of values should be used. The number of scenarios is usually based on the amount of uncertainty and sensitivity to changes and when these are larger, more scenarios should be explored. The range of values is usually based on a combination of the evidence, the clinical relevance of different values and the distributional characteristics of the parameter. For example, it would be common to base the overall range on the range of values seen for a parameter seen across a wide range of studies or to base it on the hypothetical 95% confidence interval for the parameter based on previous data or a pilot study. For effect size, clinically relevant values will tend to be an important consideration for which range of values to consider.
However, it is important to note that there is no set rules for which scenarios should be considered for a sensitivity analysis and thus sufficient consideration and consultation should be used to define the breadth and depth of sensitivity suitable for the sample size determination in your study.
A sensitivity analysis for the example above is shown below. Here, the standard deviation in the group receiving the new treatment is varied, to assess the effect on the sample size required in that group. The sample size in the control group remains at 90, and we are always aiming for 90% power. The plot shows that as the standard deviation increases, the sample size required increases dramatically. If the standard deviation is underestimated, a larger sample size is required to reach 80% power, and thus the trial will be under powered.
For σ= 1.5, 1 = 142, while for σ= 2.0, 1 = 253. This shows the importance of estimating the standard deviation as accurately as possible in the planning stages, as it has such a large impact on sample size and thus power.
Though sensitivity analysis provides a nice overview of the effect of varying the effect size or other analysis parameters, it does not present the full picture. It usually only involves assessing a small number of potential alternative scenarios, with no set official rules for choosing scenarios and how to pick between them.
How can we improve upon or supplement the process of sample size determination?
A method often suggested to combat this problem is Bayesian Assurance. Although this method is Bayesian by nature, it is used as a complement to frequentist sample size determination.
What is Bayesian Assurance?
Assurance, which is sometimes called “Bayesian power” is the unconditional probability of significance, given a prior or prior over some particular set of parameters in the calculation. These parameters are the same parameters detailed in steps 2 and 3 above.
In practical terms, assurance is the expectation of the power over all potential values for the prior distribution for the effect size (or other parameter). Rather than expressing the effect size as a single value, it is expressed as a mean (the value the effect size is most likely to be - usually the value used in the traditional power calculation) and a standard deviation (expressing your uncertainty about that value). If the power is then averaged out over this whole prior, the result is the assurance. This is often framed as the “true probability of success”, “Bayesian Power” or “unconditional power” of a trial.
How does Bayesian Assurance let us explore uncertainty?
In a sensitivity analysis, a number of scenarios are chosen by the researcher, and assessed individually for power of sample size. This gives a clear indication of the merits of the individual highlighted cases, but no information on other scenarios. With assurance, the average power over all plausible values is determined by assigning a prior to one or more parameters. This provides a summary statistic for the effect of parameter uncertainty, but less information on specific scenarios.
Overall, assurance allows researchers to take a formal approach to accounting for parameter uncertainty in sample size determination and thus create an opportunity to open a dialog on this issue during the sample size determination process. The definition of the prior distribution also allows an opportunity to formally engage with previous studies and expert opinion via approaches meta-analysis or expert elicitation frameworks such as the Sheffield Elicitation Framework (SHELF).
What is an example of an Assurance/Bayesian Power calculation for assessing the effect of a new drug?
O’Hagan et al. (2005) give an example of an assurance calculation for assessing the effect of a new drug in reducing C-reactive protein (CRP) in patients with rheumatoid arthritis.
“The outcome variable is a patient’s reduction in CRP after four weeks relative to baseline,
and the principal analysis will be a one-sided test of superiority at the 2.5%
significance level. The (two) population variance … is assumed to be … equal to
0.0625. … the test is required to have 80% power to detect a treatment effect of 0.2,
leading to a proposed trial size of n1 = n2 = 25 patients …"
For the calculation of assurance, we suppose that the elicitation of prior information … gives the mean of 0.2 and variance of 0.0625. If we assume a normal prior distribution, we can compute assurances with m = 0:2, v = 0.06 … With n = 25, we find assurance = 0.595.”
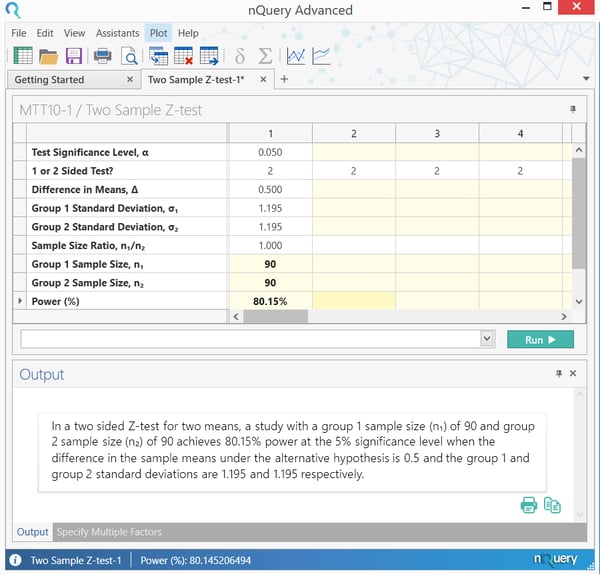
The calculation of sample size, and subsequently assurance, can be demonstrated easily in nQuery. The sample size calculation again used the “Two Sample Z-test” table.

This calculation shows that a sample size of 25 per group is needed to achieve power of 80%, for the given situation.
The assurance calculation can then be demonstrated using the “Bayesian Assurance for Two Group Test of Normal Means” table. To view the list of Bayesian Sample Size Procedures in nQuery, click here.
Start your 14 day free trial of nQuery
nQuery is the standard for fixed-term, Bayesian & Adaptive trials