Adaptive Clinical Trial Design Software
Adaptive trials can reduce the length and cost of your trial

More efficient, informative & ethical adaptive clinical trials
Reduce Trial Costs
Use adaptive designs like group sequential design to facilitate early interim decisions to ensure an efficient and ethical conclusion to your trial.
Ensure Trial Success
Avoid under or overpowered trials by using sample size re-estimation to adjust the sample size based on your blinded or unblinded interim results.
Design Complex Trials
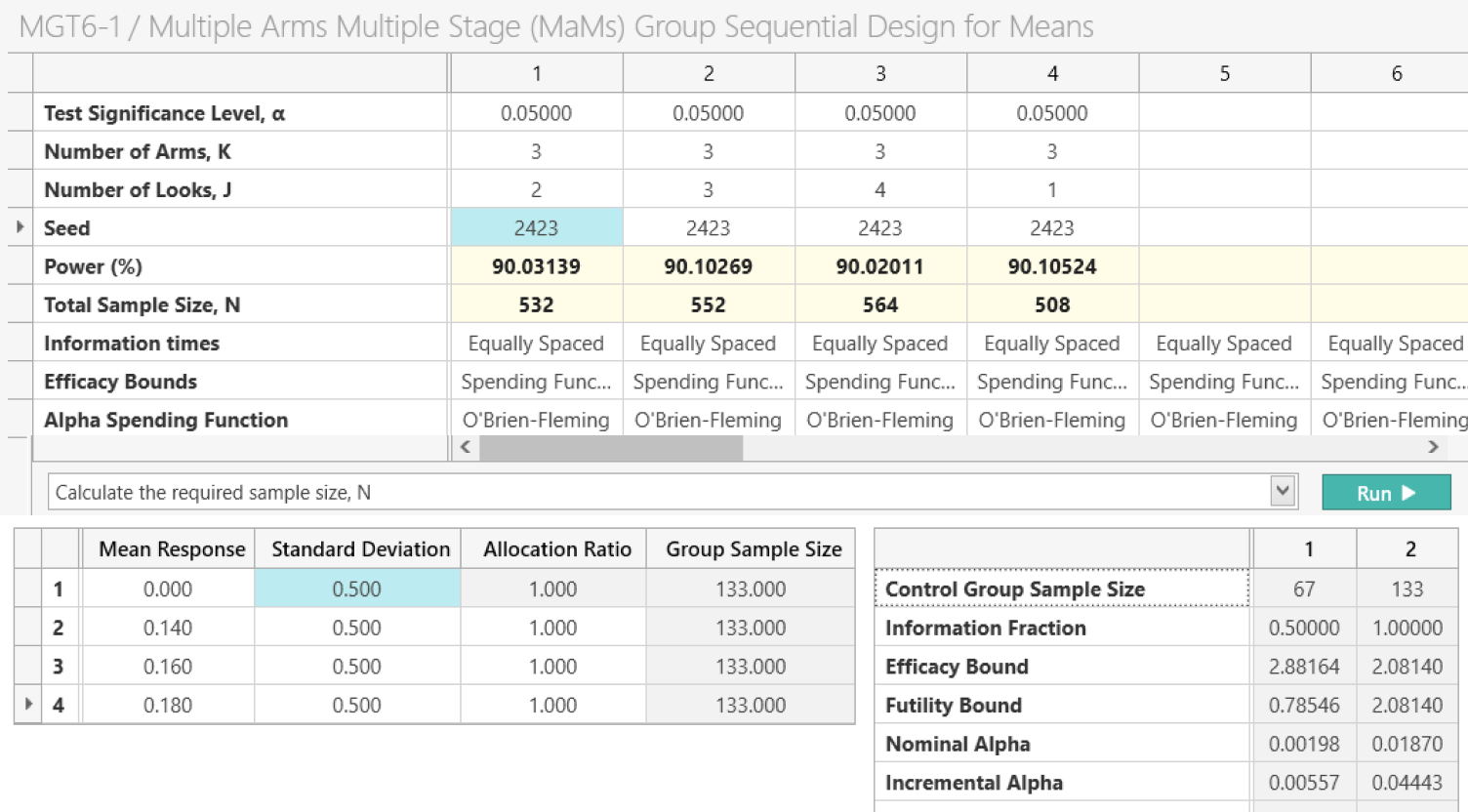
Investigate multiple treatments and dynamically drop or add trial arms using multi-arm, multi-stage (MAMS) designs
Use nQuery Adapt to optimize your sample size for sophisticated adaptive clinical trials
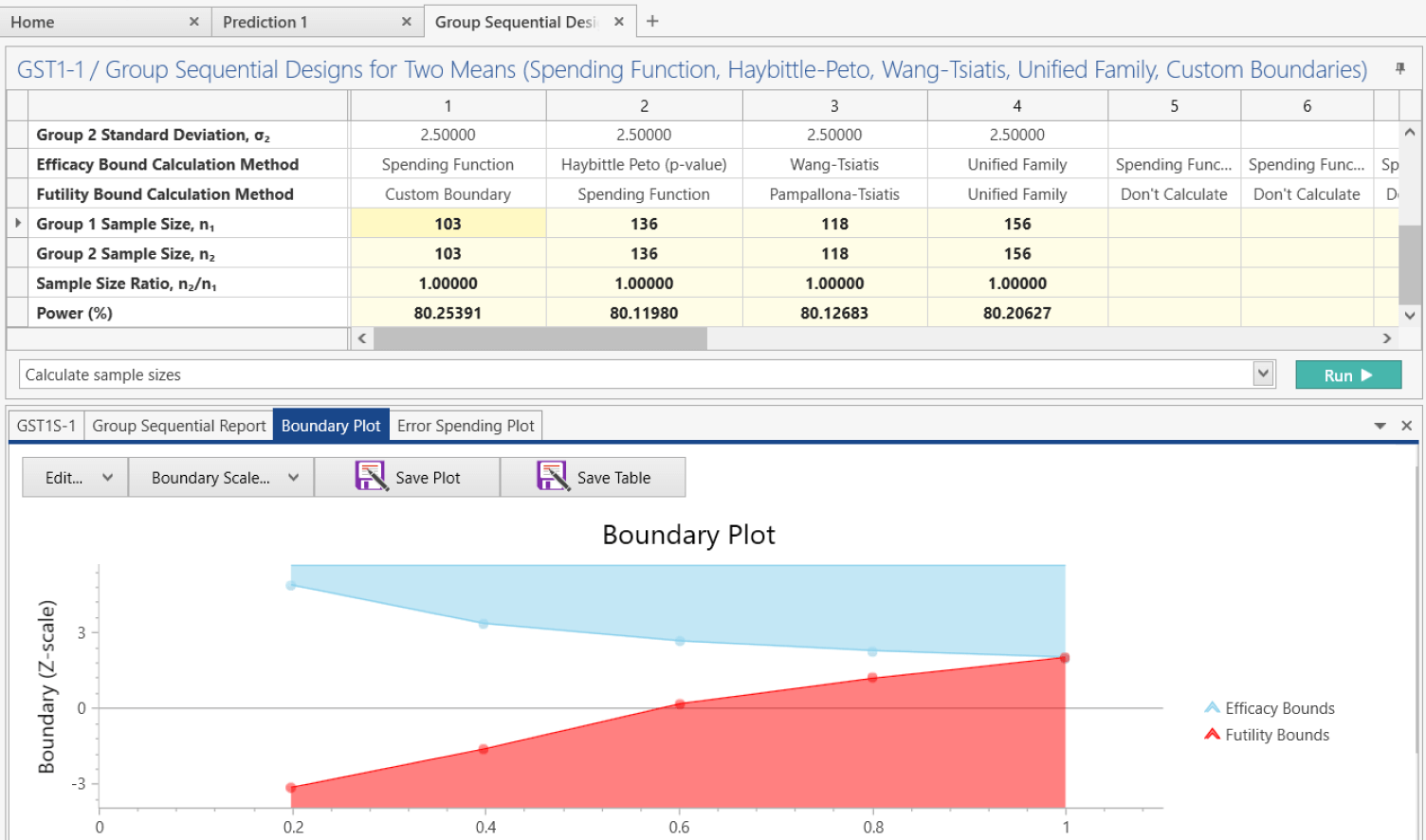
Group Sequential Design
Stop trials early using spending function, Wang-Tsiatis, Haybittle-Peto and more
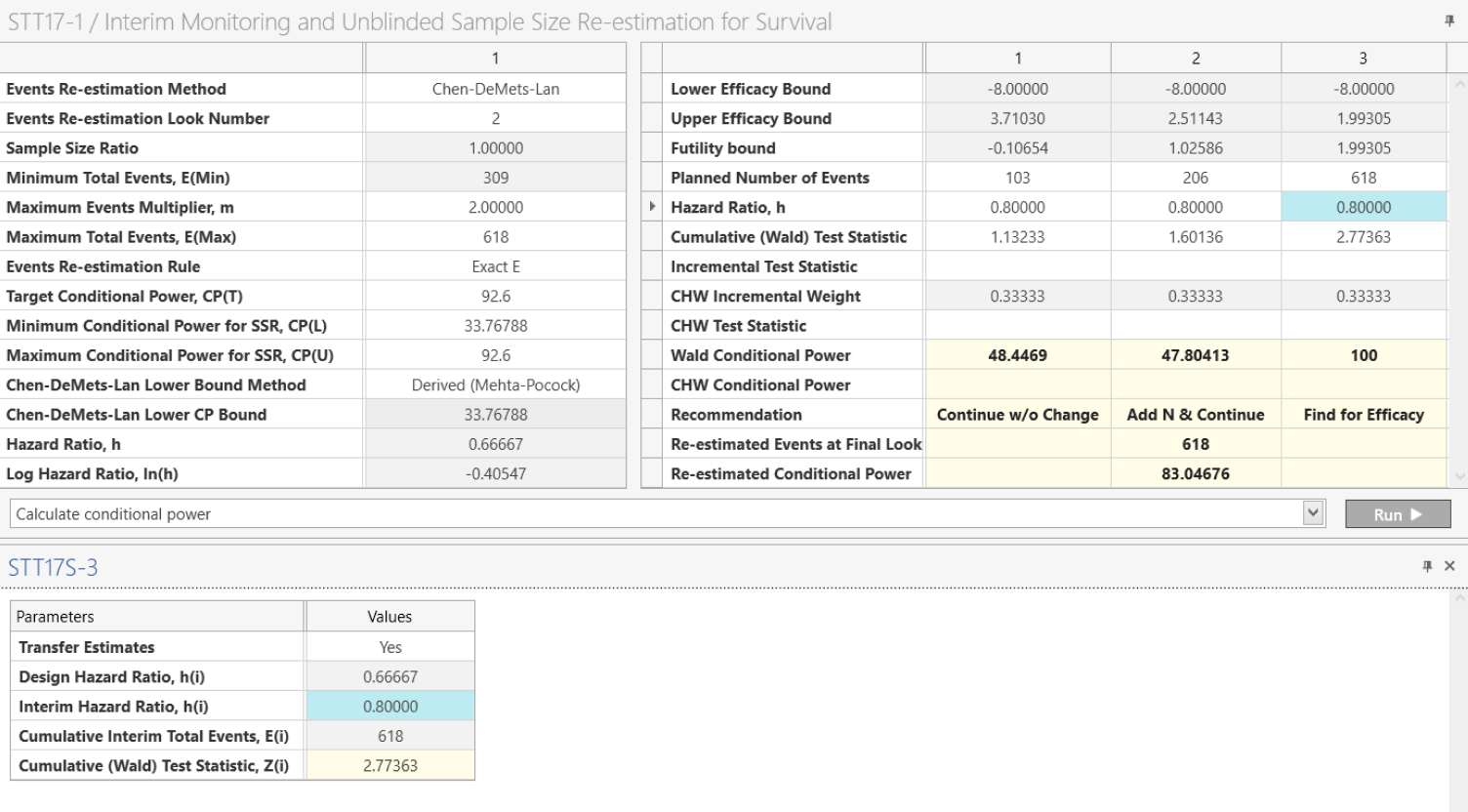
Sample Size Re-estimation
Adjust sample size dynamically using promising zone or internal pilot designs
Multi-Arm Multi-Stage (MAMS)
Evaluate multiple treatments while dropping or adding study arms
Adaptive Phase IIa Designs
Reject unpromising treatments faster using methods such as Simon’s Design
MCP-Mod
Combine Phase IIa/IIb evaluations for superior evidence for Phase II trials
Conditional Power
Find the probability of success at each interim analysis
Frequently Asked Questions
Why nQuery is used for a wide range of adaptive designs
What is nQuery Adapt?
nQuery Adapt is the powerful adaptive module of the nQuery platform for clinical trial design.
nQuery has 1000+ validated statistical procedures covering Adaptive, Bayesian and classical clinical trial designs.
With nQuery you can:
How do I take a trial?
You can take a free 14-day nQuery here.
How do I purchase?
nQuery Adapt is included in our Pro Tier.
In addition to the Adapt module, you also have access to all the popular frequentists and a Bayesian trial design functionality. With access to over 1000+ sample size scenarios.
You can purchase online here.
Have A Question?
You can get in contact with us here.
More about the Adaptive module in nQuery
Are Adaptive designs more efficient?
Are Adaptive designs more efficient?
Adaptive designs allow clinical trials to be more flexible by utilising results accumulated in the trial to change the trial’s course. Trials with an adaptive design are usually more efficient, informative and can be more ethical than trials that have a traditional fixed design because they often make better use of resources such as time and money, and may require fewer participants.
Adaptive designs can also be potentially less efficient than a fixed term trial or simple adaptive design if designed poorly. For example, sample size re-estimation designs lead to higher average sample sizes for minimal success rate increases or adaptive selection designs which include additional arms with minimal prior chance of succeeding.
Overall, adaptive designs when properly considered and well-planned have considerable scope for increasing trial efficiency but the additional flexibility could mean more opportunities for making poor design decisions.
Recommended:
How to Calculate Sample Size for Group Sequential Designs
What is a Group Sequential Design?
What is a Group Sequential Design?
Group sequential designs are the most widely used type of adaptive trial in confirmatory Phase III clinical trials. Unlike standard fixed-term trials, group sequential designs allow a trial to end early based on pre-specified interim analyses for efficacy or futility. This is achieved through an error spending method, which allocates a portion of the total Type I (efficacy) or Type II (futility) error at each interim analysis. The ability to end a trial early can help reduce costs, accelerate approval of effective treatments, and discontinue trials with poor outcomes.
What is the assessment of futility in clinical trials?
The term 'futility' refers to the inability of a clinical trial to achieve its aims. In practice, this means ending a clinical trial early when interim results indicate it is highly unlikely to reach statistical significance. Assessing futility allows researchers to conserve resources and redirect efforts toward more promising studies.
Recommended:
How to Calculate Sample Size for Group Sequential Designs
What are Group Sequential and Promising Zone Designs?
What are Group Sequential and Promising Zone Designs?
Group Sequential and Promising Zone Designs are adaptive clinical trial methods that allow researchers to conduct interim analyses and make data-driven modifications—such as early stopping or sample size re-estimation—without compromising the trial's integrity or statistical power.
How does nQuery support Group Sequential Designs?
nQuery's Group Sequential Design tools enable you to calculate stopping boundaries, evaluate interim results, and increase sample size based on conditional power. These features enhance flexibility, improve efficiency, and help rescue promising trials that might otherwise fail.
What is Conditional Power?
Conditional power is the probability of rejecting the null hypothesis at a future analysis point, given the current interim results and an assumed true effect size—typically based on initial or interim estimates.
What is Predictive Power?
Predictive power, or Bayesian Predictive Power, is the average of conditional power across the posterior distribution of the effect size. It reflects uncertainty in the true effect and is often viewed as a more robust indicator of trial success.
Recommended:
Explore more in our guide:
How to Calculate Sample Size for Group Sequential Designs
What is sample size re-estimation (SSR)?
What is sample size re-estimation (SSR)?
Sample size r-estimation (SSR) is a type of adaptive trial where one can change the sample size if required. Sample size determination is a pre-trial process that will be conducted on the basis of inherently uncertain planning parameters (e.g. variance, effect size) and thus changing the sample size based on improved interim estimates for these parameters is an obvious adaptation target.
SSR can ensure that sufficient power is obtained for promising results in an underpowered study or could ensure more patients receive the superior treatment or transition directly from one trial phase to another. Combined this may reduce the use of resources and time or improve the likelihood of success of the trial.
There are two primary types of SSR: Unblinded SSR and Blinded SSR. The main differences between these designs are that they differ on whether the data is blinded or not and the planning parameter targeted to for an improved interim estimate.
Recommended Viewing:
[Video] Learn How To Use Adaptive design features in nQuery
Conditional vs Predictive power?
What is conditional power?
Conditional power is the probability that the trial will reject the null hypothesis at a subsequent look given the current test statistic and the assumed “true” parameter values, which are usually assumed to equal their interim estimates or their initial planning values.
What is predictive power?
Predictive power (also known as Bayesian Predictive Power) is the conditional power averaged over the posterior distribution of the effect size. It is commonly used to quantify the probability of success of a clinical trial. It has been suggested as a superior alternative to conditional power as it treats the “true” estimates as uncertain rather than fixed.
Recommended:
An Introduction to Adaptive Clinical Trial Designs
Recommended Resources
Get started with nQuery today
Start for free and upgrade as your team grows














