Sample Size for Bayesian Statistics
Use Assurance to understand uncertainty in your sample size & find sample size for Bayesian methods
Understand & Tackle Trial Uncertainty
Find the True Probability of Success
Calculate Bayesian assurance to better understand the true probability of success for your trial given parameter uncertainty.
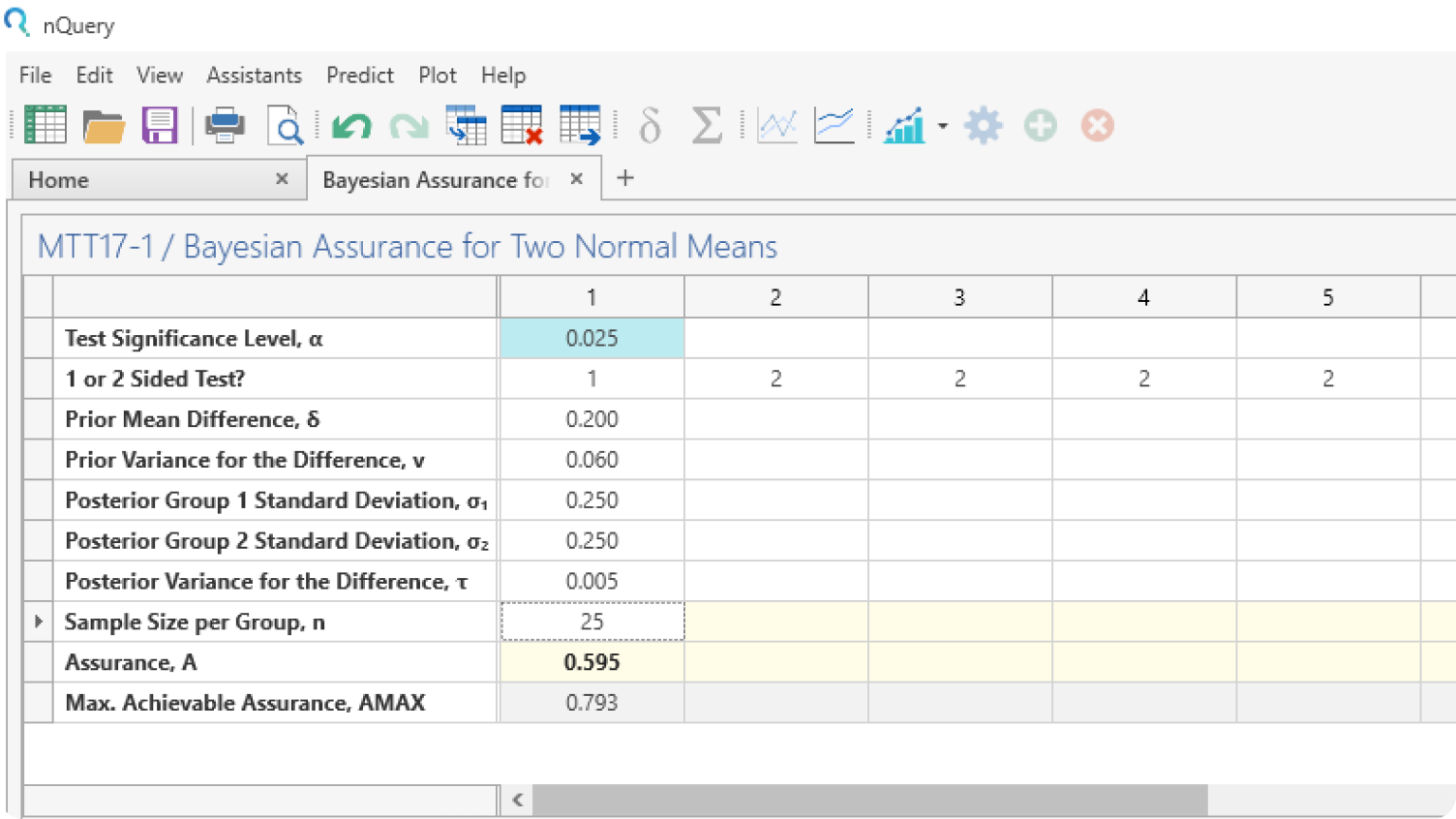
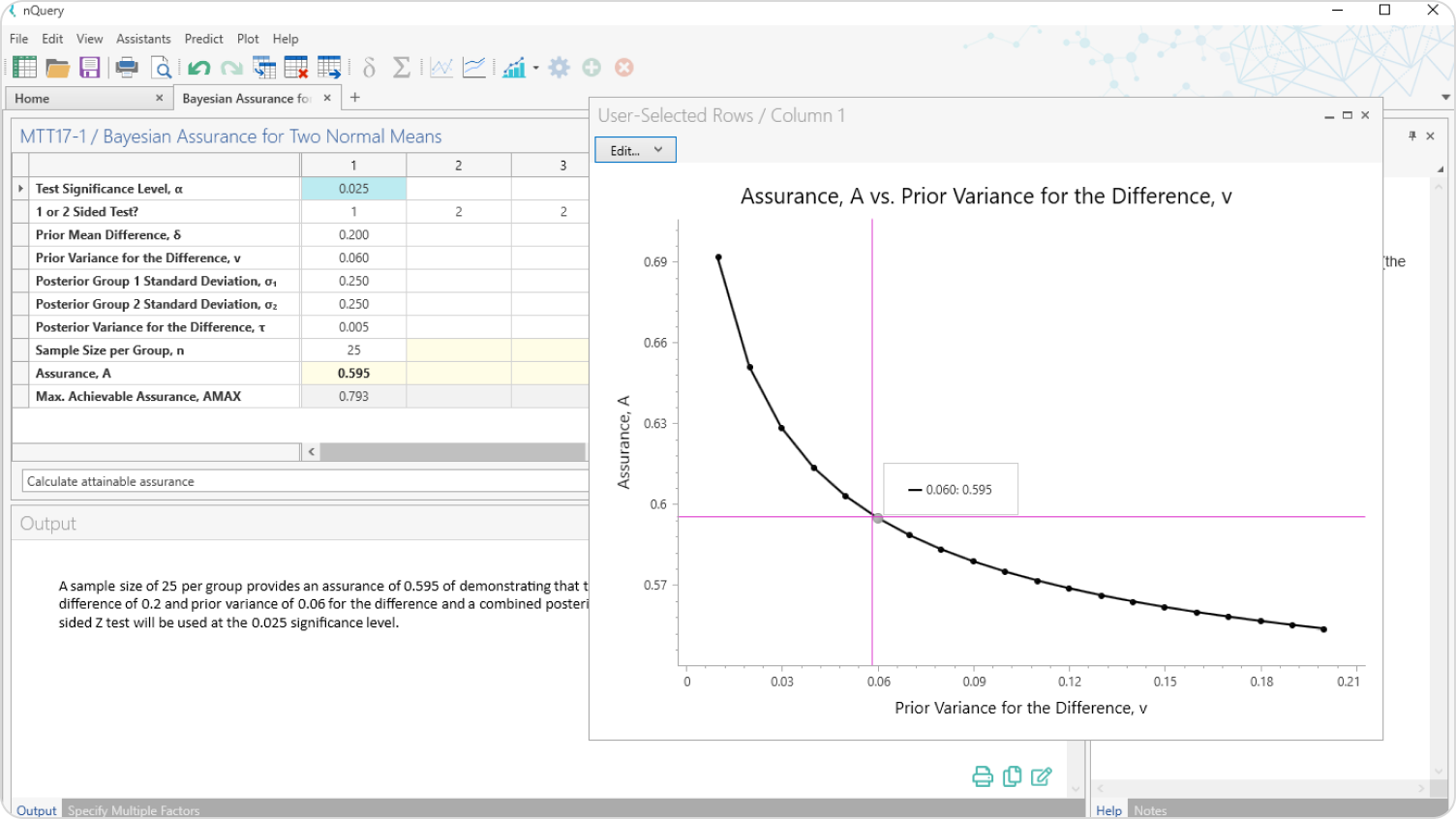
Plot Bayesian Uncertainty
Use the graphing tools to explore the effect of prior uncertainty on the required sample size and easily share your conclusions with all trial stakeholders.
Integrate Prior Data
Use existing data in your sample size calculations for Bayesian methods such as credible intervals, posterior errors and Bayes Factors
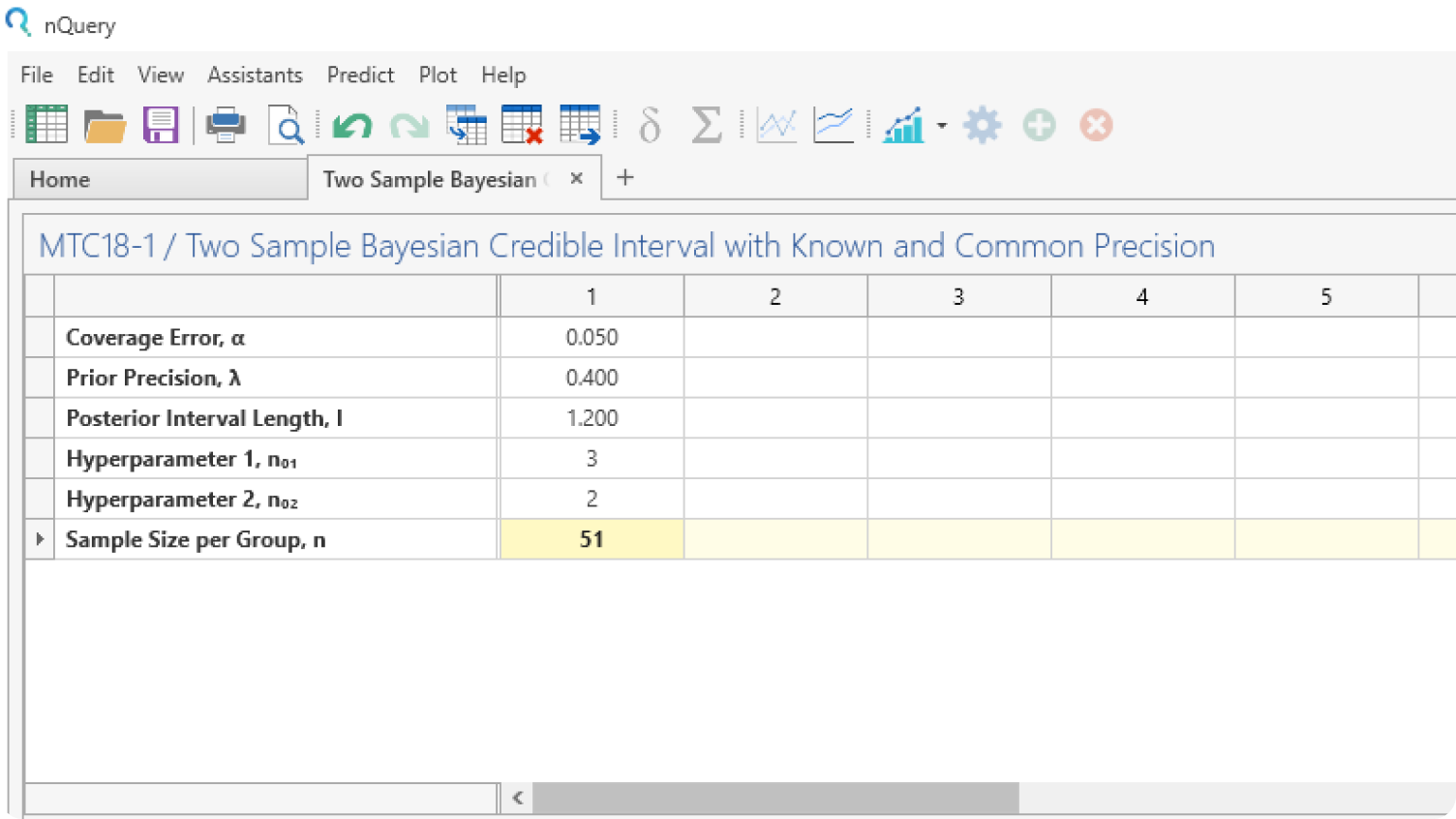
Use nQuery Bayes to combine prior knowledge + real-world data to make informed decisions
Bayesian Assurance
Find the true probability of success for you clinical trial using assurance
Bayesian Intervals
Sample size for credible interval width for a variety of priors and endpoints
Bayes Factors
Compare the probability of statistical hypotheses directly
Bayesian Testing
Test for treatment effect using Posterior Errors or Bayesian Average Effects
Predictive Power
Find the interim probability of success adjusted for parameter uncertainty
Phase I Designs
Sample size for methods such as the continual reassessment method (CRM)
Bayesian Sample Size Determination
Bayesian Analysis continues to grow in popularity due to the ability to integrate prior knowledge and its intuitive interpretation

Frequently Asked Questions
What is nQuery Bayes?
nQuery Bayes is the powerful Bayesian module of the nQuery platform for clinical trial design.
nQuery has 1000+ validated statistical procedures covering Adaptive, Bayesian and classical clinical trial designs.
How do I take a trial?
You can take a free 14-day nQuery here.
How do I purchase?
nQuery Bayes is included in our Plus Tier.
In addition to the Bayes module, you also have access to over 1000+ sample size scenarios.
You can purchase online here.
Have A Question?
More about the Bayesian module in nQuery
The growth of Bayesian analysis in clinical trials
What is Bayesian statistics?
Bayesian statistics is a field of statistics based on the Bayesian interpretation of probability where probability expresses a degree of belief in an event that changes as new information is gathered rather than a fixed value based upon frequency or propensity. The degree of belief will be based on our prior knowledge about the event, such as the results of previous experiments, or personal beliefs about the event and the data up to that given point.
Why is Bayesian analysis becoming more popular in clinical trials?
Bayesian analysis is becoming a more and more popular form of statistical analysis for clinical trials. This is because it offers the ability to integrate domain knowledge and prior study data in order to improve the efficiency and accuracy of testing and estimations. There are also arguments that the Bayesian framework better reflects real-world treatment decision-making.
Recommended Viewing:
Bayesian Approaches to Interval Estimation & Hypothesis testing
Bayesian statistics & sample size determination
How are Bayesian statistics applied in sample size determination?
There are two broad areas where Bayesian approaches are being applied to sample size determination.
These are:
-
Sample Size for Bayesian Methods: This is when you are planning to use a Bayesian test or statistical method and require a sample size estimate to get the desired “success” probability for this method. Examples of this would be determining the required sample size for a sufficiently high Bayes Factor, sample size for a sufficiently narrow credible interval and sample size methods based on decision-theoretic approaches using approaches such as utility functions.
-
Using Bayesian approaches to improve existing sample size methods: These methods integrate Bayesian analysis and thinking when the planned analysis is frequentist in order to add greater context to the frequentist sample size determination or improve upon the characteristics of the current sample size method. Examples of this are Bayesian Assurance, Predictive Power, Posterior Error Methods and using Bayesian Adaptive Designs adaption criteria.
Recommended Viewing:
Benefits of Bayesian Assurance in clinical trials
What are the benefits of Bayesian Assurance?
Bayesian Assurance - The True Probability of Success
Using the Bayesian module in nQuery and a framework such as SHELF leads to a
Identify Study Design Threats & Opportunities
Bayesian Techniques such as Prior Elicitation provides a systematic approach to reduce the analysis gap between completed studies and planned studies when there is a lack of reliable evidence or scientific consensus.
Examining experts prior distribution may often reveal concerning aspects of the study design that was previously overlooked.
The elicited prior distribution can be used to assess various study designs. These can ultimately be influential in the appropriate ‘go’ or ‘no go’ decision.
The elicitation process highlights not only the rationale for believing in the likely effect of the
Communicate Complex Findings to Non-Statisticians
The prior elicitation process is methodically and scientifically-driven. It enables a more vigorous review of data and decision making.
A more robust understanding of risks and insights means these can be formally acknowledged and plans made to mitigate these risks to reduce costs and thus reduce the likelihood of failure.
Being able to formally capture internal and expert opinion, integrate existing data and identify obstacles in the study protocol, teams can provide boards with formally appropriate estimates of the probability of trial success as well as robust plans for interim decision rules where appropriate, enabling better portfolio and company-wide decision making.
Recommended Viewing:
Why to include Bayesian statistics when planning your frequentist trial [Webinar]
Confidence interval Vs Credible interval
What are the differences between a confidence interval and a credible interval
Posterior credible Intervals are the most commonly used Bayesian method used in interval estimation. Credible Intervals are seen by many as being superior to confidence intervals as they give the probability that the interval contains the true value of the parameter. This is often seen as the more naturalistic interpretation of what a statistical interval should do.
When confronted with the problem of trying to specify a reasonable statistical interval given an observed sample, the frequentist and Bayesian approaches differ.
A confidence interval is the frequentist solution to this problem. Under this approach, you assume that there is a true, fixed value of the parameter. Given this assumption, you use the sample to get to an estimate of this parameter. An interval is then constructed in such a way that the true value for the parameter is likely to fall in this interval with a given level of confidence (say 95%).
A credible interval on the other hand is the Bayesian solution to the above problem. It is defined as the posterior probability that the population parameter is contained within the interval. In this case the true value is, in contrast to the above, assumed to be a random variable. In this way the uncertainty about the true parameter value is captured by assuming a certain prior distribution for the true value of the parameter. This prior distribution is then combined with the obtained sample and a posterior distribution is formed. An estimate of the true parameter value is then obtained from this posterior distribution. A credible interval is then formed to contain a given proportion of the posterior probability for the parameter estimate. This can be interpreted that a given interval has a given probability of containing the true parameter value.
Recommended Viewing:
Bayesian Approaches to Interval Estimation & Hypothesis testing
Recommended Resources
Get started with nQuery today
Start for free and upgrade as your team grows














